Research areas
Faculty members are involved in a diverse range of research topics. Here is a list of sample projects for each group. For more information, please visit faculty members' homepages.
Our research group interests are mainly focused on the numerical methods for PDEs using spectral/pseudospectral methods, radial basis function methods, discontinuous Galerkin discretizations, uncertainty quantification, and reduced basis methods.
Group members include:
- Yanlai Chen, whose sample projects are
Project title Project picture Project description Design and analysis of various reduced basis method 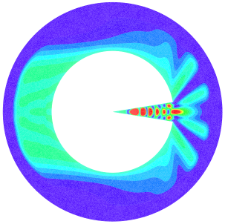
RBM-simulation of the electromagnetic scattering of a Pacman-shaped object
Models of reduced computational complexity is indispensable in scenarios where a large number of numerical solutions to a parametrized problem are desired in a fast/real-time fashion. Reduced basis method (RBM) can improve efficiency in this scenario by several orders of magnitudes. The accuracy of the RBM solution is maintained through and the construction of the surrogate solution space is guided by an error estimation mechanism.
This project is about designing highly efficient and practically implementable RBM for challenging contexts involving high dimensionality, nonlinearity, fractional derivative order, non-Gaussian stochasticity, etc.
Hybridizable discontinuous Galerkin (HDG) Method 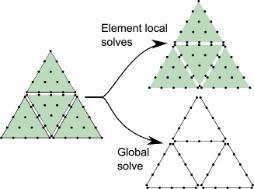
(Picture credit: M.P. Ueckermann and P.F.J. Lermusiaux)
The development of HDG methods was motivated by the desire to improve the computational efficiency (and as a consequence, the accuracy) of the more modern discontinuous Galerkin (DG) compared to the traditional finite element method (CG) for elliptic problems.
These projects (with B. Dong) are mainly concerned about the theoretical analysis (stability, accuracy, conservativity etc) of HDG when it is applied to high order equations. We are also interested in efficient implementations realizing the huge potential of HDG for challenging problems.
Interesting applications of RBM 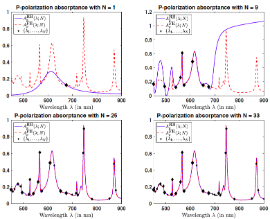
RBM-simulation of the absorptance of a thin film solar cell
This series of projects focuses on applying/adapting RBM for various application domains such as thin film solar cell (with P. Monk, M. Solano), battery design (with L. Ji, Z. Xu), and internal engine combustion (with M. Raessi), etc. We are also exploring promising nascent topics like layered neural networks and high-dimensional data analytics as testing beds for incorporating RB-inspired ideas. - Zheng Chen, whose sample projects are
Project title Project picture Project description - Gary Davis, whose sample projects are
Project title Project picture Project description Constructing typologies of pain questions and issues from forums (with Matthew Cormier)
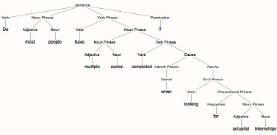
Mathematica-produced tree structure of a question from a Reddit forum
In starting a business venture it is vitally important to identify potential customers and their specific problems. A productive business venture then sets out to solve those problems and so develop repeat customers. One way to discover questions from, problems of, and issues for, potential customers is through discussion forums, particularly, but not exclusively, those on Reddit. This project is aimed at automating the process of identifying such questions, problems and issues, through data scraping and computational linguistic analyses of text. The immediate aim is to develop a typology of questions, both general and domain specific.
Convergence in the Wythoff array (with Alfa Heryudono)
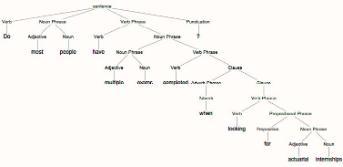
The Wythoff array
The Wythoff array is an array of positive integers that has a countably infinite number of rows and columns. It is an example of an interspersion array, and arises from considerations of the coordinates of winning positions in Wythoff's game. It is related to Zeckendorf’s representation of positive integers as sums of Fibonacci numbers. The ratio of successive terms in any row of the Wythoff array is easily seen to converge to the golden mean, since the rows are determined, after two initial entries, by a Fibonacci type recurrence. The diagonal of the array is more problematic, and we have made both computational and some proof progress in determining the rate of convergence of successive diagonal terms of the Wythoff array.
- Bo Dong, whose sample projects are
Project title Project picture Project description - Scott Field, whose sample projects are
Project title Project picture Project description - Sigal Gottlieb, whose sample projects are
Project title Project picture Project description - Alfa Heryudono, whose sample projects are
Project title Project picture Project description - Cheng Wang, whose sample projects are
Project title Project picture Project description
Our group is interested in different aspects of theoretical and computational gravitational physics.
Group members include:
- Scott Field, whose sample projects are
Project title Project picture Project description
Our research group studies ways in which students at all levels, K-20, can engage more deeply with mathematical thinking through computational approaches. We seek to understand how students and teachers respond to serious mathematical and scientific questions that involve extensive computation, and what sorts of computational investigations are feasible for students at different stages of development.
Group members include:
- Gary Davis, whose sample projects are
Project title Project picture Project description The nature of memory for mathematical reasoning and proof

An example of explanative memory by a 6th grade student
Memory for mathematical arguments and proof seems to have the characteristics of a memory system, as described by Schacter, D., Wagner, A. & Buckner, R. (2000). Memory systems of 1999, Oxford Handbook of Memory, pp. 627-643. This project is based on empirical work with middle school students and undergraduates, and attempts to demonstrate rigorously that memory for mathematical arguments is indeed a new memory system – explanative memory - in addition to such well-known memory systems as working memory, semantic memory, episodic memory, the perceptual representation system, and procedural memory.
A primer on memory for mathematics teachers
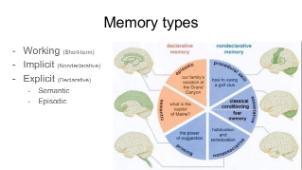
Schematic of different memory systems
Mathematics teachers are known to lament “Why can’t students just memorize it?” Questions such as this demonstrate a profound lack of knowledge of findings in the neuroscience of memory since the 1990s. In this project we are developing an account of the functioning of human memory systems and the importance of understanding those for mathematics teaching and productive long-term student memory for mathematics.
- Adam Hausknecht, whose sample projects are
Project title Project picture Project description - Saeja Kim, whose sample projects are
Project title Project picture Project description
Data science is an interdisciplinary research effort in data-intensive methodologies and applications. Research focuses on data collection, analysis, and visualization in diverse application areas. Some of these areas include artificial intelligence, autonomous mobile robotics, nursing informatics, bioinformatics, and scientific data management and reproducibility.
Group members include
- Zheng Chen, whose sample projects are
Project title Project picture Project description - Gary Davis, whose sample projects include
Project title Project picture Project description Implementation and analysis of a sophomore level client-consulting course in exploratory data analysis (with Turner Bohlen, Matthew Cormier, James Tanton & Donghui Yan)
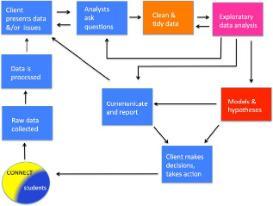
Schematic of the process of exploratory data analysis for a client
The course will be implemented in MTH 231 Exploratory Data Analysis in Fall 2018, and will be based on a client consultancy model. To date 4 faculty members have offered data in the areas of: (a) student completion rates in the University’s Connect program, (b) 12000+ legislative bills introduced in 10 states over a 3 year period, (c) percent cover of plant species and environmental conditions like temperature, light, wind, and soil microbial community, collected over four years from a set of about 100 plots on dunes at Waquoit Bay, (d) massive fat-tailed simulations of where nuclear detonations are likely to take place in supernovae. The basic research issues are: the impact of the course structure on students, clients and the instructor; the dynamics of the client-student interactions over the semester; the quality of student analytical reports; and the nature, depth, utility, and productivity for statistical analysis of student- generated questions. The questioning aspect of this research will be carried out in partnership with Beagle Learning.
- Scott Field, whose sample projects are
Project title Project picture Project description - Donghui Yan, whose sample projects include
Project title Project picture Project description
This group studies the development of mathematical methods for application to problems in physics.
Group members include
- Dana Fine, whose sample projects include
Project title Project picture Project description
